双曲线
我们知道:
1、到一点距离是定值的图形是圆。
2、到两点距离和是定值的图形是椭圆。
3、到两点距离差是定值的图形是双曲线。
4、到两点距离商是定值的图形是(阿氏)圆。
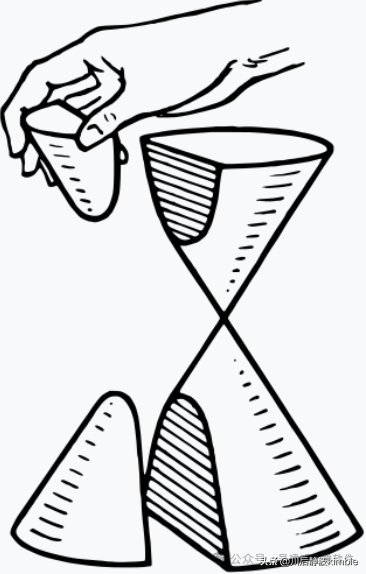
双曲线(hyperbola)是一条有两个分支的开放曲线,是一个平面与双圆锥体的两半的交点。
该平面不必平行于圆锥体的轴线;无论如何,双曲线都是对称的。
双曲线是指与平面上到两个定点的距离之差的绝对值为定值的点的轨迹,也可以定义为到定点与定直线的距离之比是一个大于1的常数的点之轨迹。
双曲线是圆锥曲线的一种,即圆锥面与平行于中轴的平面的交截线。
在光学中,双曲线被用于描述透镜和反射器的形状,以及光线的聚焦和散焦。
定义
把平面内与两个定点 F1,F2 的距离的差的绝对值等于非零常数(小于 ∣F1F2∣ )的点的轨迹叫做双曲线。
这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距。
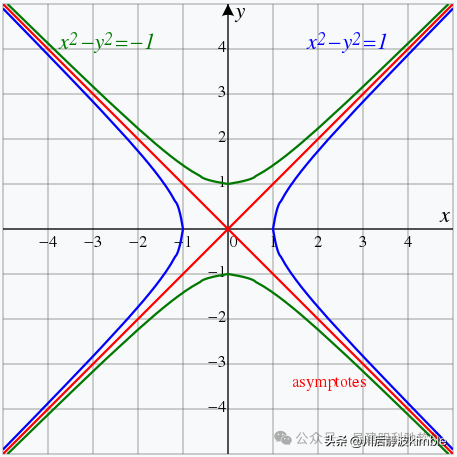
从代数上说,双曲线是在笛卡尔平面上由如下方程定义的曲线。
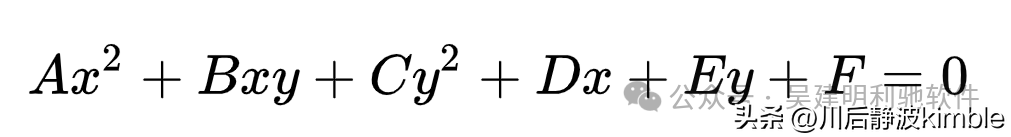
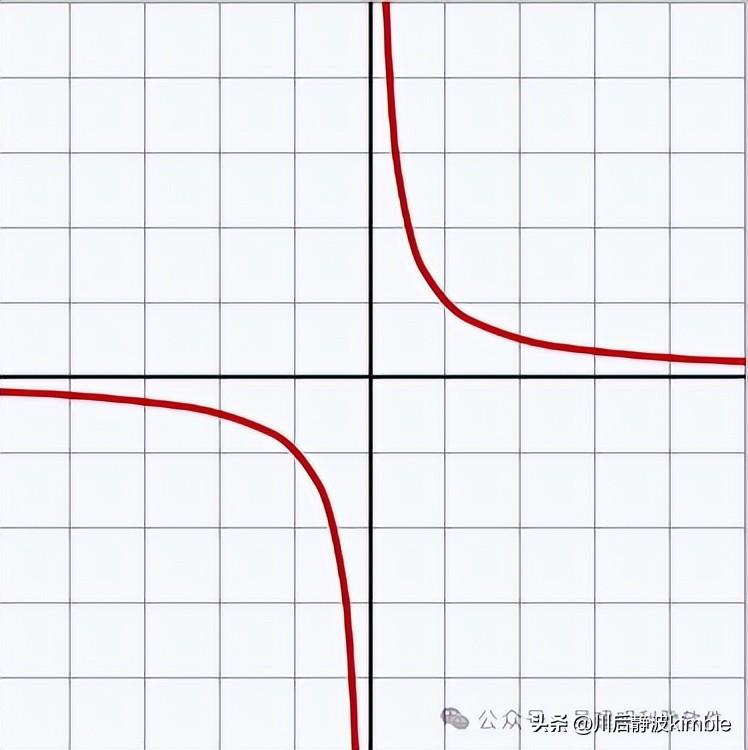
在笛卡尔坐标平面上,两个互为倒数的变量的图像也是双曲线。
比如:y=1/x
标准方程及求法
标准方程

求法

双曲线的简单几何性质

实轴、虚轴:实轴长等于2a,a叫做半实轴长;虚轴长等于2b,b叫做半虚轴长
用代码绘制
import numpy as np
import matplotlib.pyplot as plt
# 定义参数a和b
a = 2
b = 1
# 生成x的取值范围
x = np.linspace(-5, 5, 1000)
# 根据标准方程计算y的值
y = b * np.sqrt(1 + (x**2 / a**2))
# 绘制双曲线的上半部分
plt.figure(figsize=(10, 5))
plt.plot(x, y, label='Hyperbola', color='blue')
plt.plot(x, -y, color='blue') # 绘制双曲线的下半部分
plt.xlabel('x')
plt.ylabel('y')
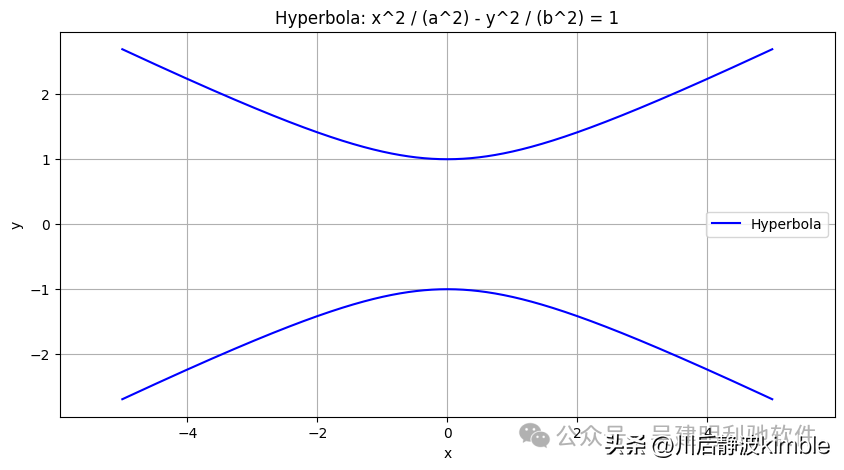
plt.title('Hyperbola: x^2 / (a^2) - y^2 / (b^2) = 1')
plt.legend()
plt.grid(True)
plt.axis('equal')
plt.show()效果如下: