幂函数是我们在数学学习中常接触到的一类函数,它们不仅有着重要的理论意义,同时也在生活中扮演着至关重要的角色。比如,幂函数可以用来描述物体加速度、农田作物产量与耕地面积之间的关系等。本文将会为您详细介绍幂函数的定义、性质及其在实际应用中的表现,希望能够激发您对幂函数的兴趣,并加深对其知识内容的理解。
01 幂函数简介
幂函数是一种基本的代数函数,它表示成 f(x) = x^a 的形式,其中 x 是自变量,a 是实数指数。幂函数的图像特征与指数 a 的正负有关,当 a>0 时,幂函数是单调递增的,而且在 x=0 处有一个导数为 0 的极小值点 (0,0);当 a<0 时,幂函数是单调递减的,并且没有实零点;当 a=0 时,幂函数是常数函数 f(x)=1。此外,当自变量 x 取负值时,幂函数会出现奇偶性变化,当 a 为奇数时幂函数是奇函数,当 a 为偶数时幂函数是偶函数。
例如,考虑指数 a=2 时的幂函数 f(x)=x^2,它的图像如下所示:
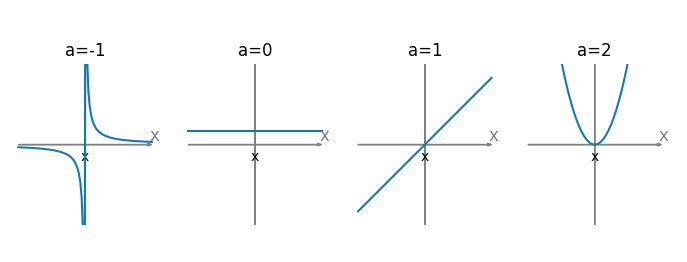
从图像中可以看出,当 a>0 时,幂函数是单调递增的,图像开口向上,且过点 (1,1)。当 0<a<1 时,函数在 x 轴上方,逐渐向 x 轴靠近;当 a<0 时,函数在 x 轴下方,逐渐向 x 轴靠近。当 a=0 时,幂函数恒等于 1。

02 幂函数的性质
2.1 单调性
幂函数的单调性是指函数取值随着自变量变化的增大或减小而单调递增或递减。具体地,当指数 a > 0 时,幂函数 f(x) = x^a 是单调递增的;当指数 a < 0 时,幂函数 f(x) = x^a 是单调递减的。
例如,考虑指数 a=3 的幂函数 f(x)=x^3,它的图像如下所示:
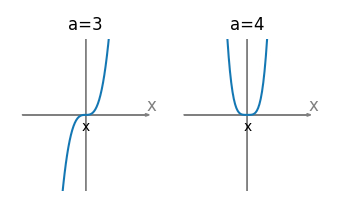
从图像中可以看出,当 a>0 时,幂函数的图像是开口向上的拟物线,函数值随着自变量 x 的增大而增大。当 a<0 时,幂函数的图像是开口向下的拟物线,函数值随着自变量 x 的增大而减小。
2.2 奇偶性
幂函数的奇偶性是指函数关于 y 轴或原点的对称性质。具体地,当指数 a 是整数时,幂函数 f(x)=x^a 是关于原点对称的奇函数;当指数 a 是正偶数时,函数 f(x)=x^a 是关于 y 轴对称的偶函数。
例如,考虑指数 a=4 的幂函数 f(x)=x^4,它的图像如下所示:

从图像中可以看出,当 a 为正偶数时,幂函数的图像是关于 y 轴对称的。因此,在 x>0 和 x<0 的情况下函数值相等,即 f(-x)=f(x),表明幂函数是偶函数。
2.3 零点
幂函数的零点是指函数曲线和 x 轴的交点横坐标。具体地,当指数 a>0 时,幂函数 f(x) = x^a 的唯一实根为 x=0;当指数 a<0 时,幂函数 f(x) = x^a 在 x 轴上没有实零点;当指数 a 是奇数时,幂函数 f(x) = x^a 有且仅有一个实零点,当指数 a 是偶数时,幂函数 f(x) = x^a 有两个实零点。
例如,考虑指数 a=-2 的幂函数 f(x)=x^{-2},它的图像如下所示:
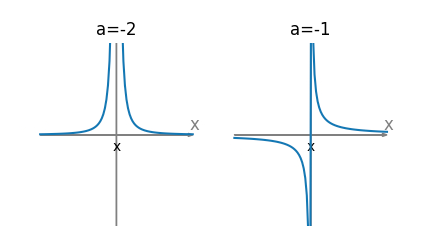
从图像中可以看出,当 a<0 时,幂函数的图像始终在 x 轴下方,没有实零点。当指数 a 是奇数时,幂函数的图像经过原点且在原点处取值为 0,因此有且仅有一个实零点;当指数 a 是偶数时,幂函数的图像关于 y 轴对称,因此存在两个实零点。
03 幂函数的应用
3.1 物理应用
幂函数在物理学中有广泛的应用。例如,牛顿第二定律表明了物体的加速度与受到的作用力成正比,而质量则是一个因子,受到作用力越大、质量越小的物体加速度越大。因此,可以将加速度看作是作用力和质量的幂函数关系。
例如,考虑物体的加速度 a 与作用力 F 和质量 m 的幂函数关系,可以表示为
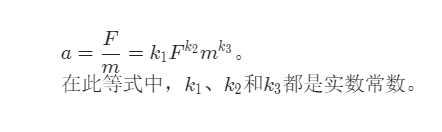
3.2 经济应用
幂函数在经济学中也有着重要的应用。例如,在生产率和投入之间的关系中,可以用幂函数来描述农田的作物产量。
例如,假设农田的作物产量 P 与耕地面积 A 成幂函数关系,即

通过分析幂函数的图像特征,我们可以预测作物产量随着耕地面积的增加而增加。

04 结语
幂函数是一类十分重要的函数,它在各个领域都有广泛的应用。通过本文的介绍,我们可以更好地了解幂函数的定义、性质和应用,为自己的学习和研究提供帮助。
