基础知识
树是一个有n个有限节点组成一个具有层次关系的集合,每个节点有0个或者多个子节点,没有父节点的节点称为根节点,也就是说除了根节点以外每个节点都有父节点,并且有且只有一个。
树的种类比较多,有二叉树,红黑树,AVL树,B树,哈夫曼树,字典树等等。
甚至堆我们也可以把它看成是一棵树,树的这么多种类中,我们最常见的应该是二叉树了,下面我们来看一下他的结构。
定义:
应用:
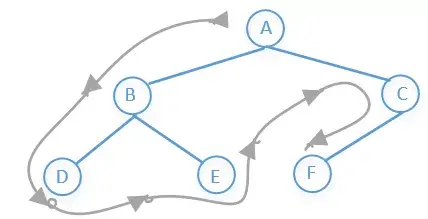
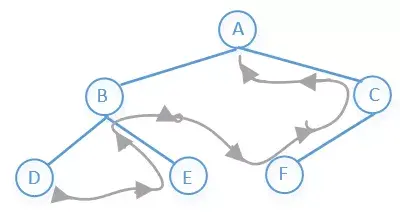
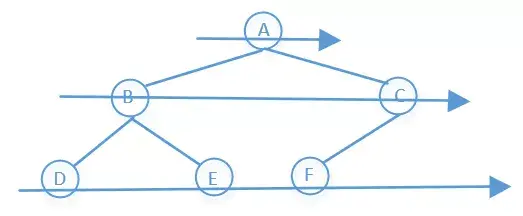
树的种类实在是太多,关于树的算法题也是贼多,这一篇文章不可能全部介绍完,我们需要具体问题再具体分析。这里主要介绍的是二叉树,并且只介绍树的一些最基础的几个算法。我们先来看个图
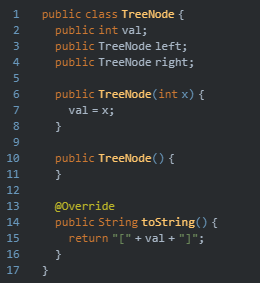
节点类
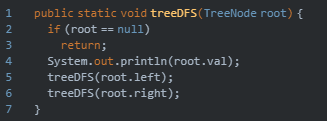
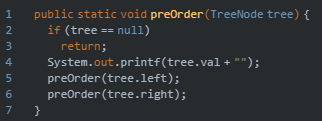
1,前序遍历
他的访问顺序是:根节点→左子树→右子树
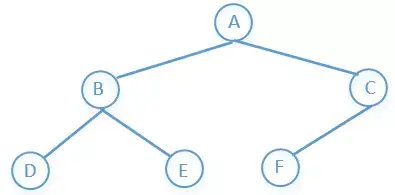
所以上图前序遍历的结果是:A→B→D→E→C→F
访问顺序如下
代码如下
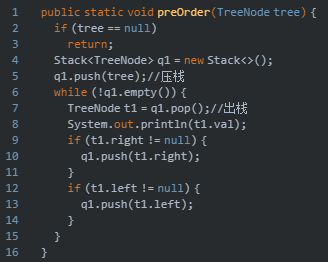
非递归的写法
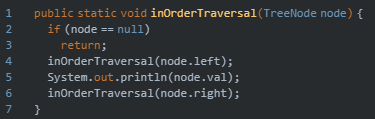
2,中序遍历
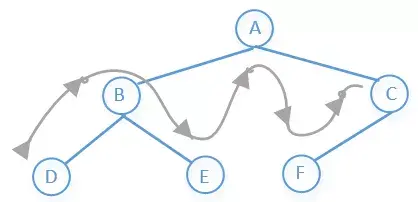
他的访问顺序是:左子树→根节点→右子树
所以上图前序遍历的结果是:D→B→E→A→F→C
访问顺序如下
代码如下
非递归的写法
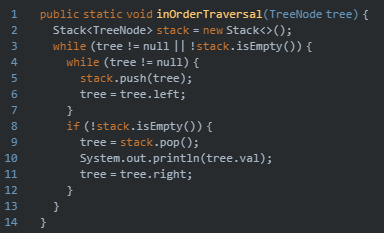
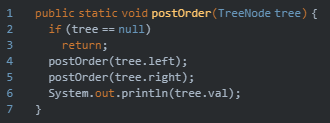
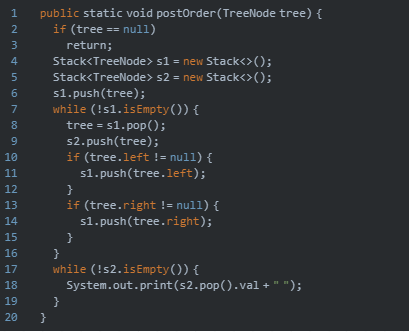
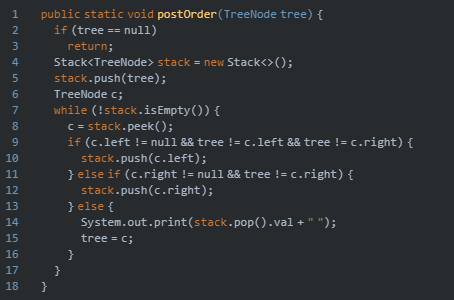
3,后序遍历
他的访问顺序是:左子树→右子树→根节点
所以上图前序遍历的结果是:D→E→B→F→C→A
访问顺序如下
代码如下
非递归的写法
或者
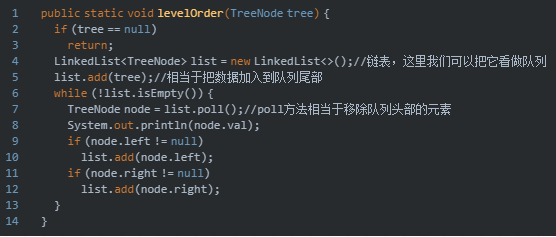
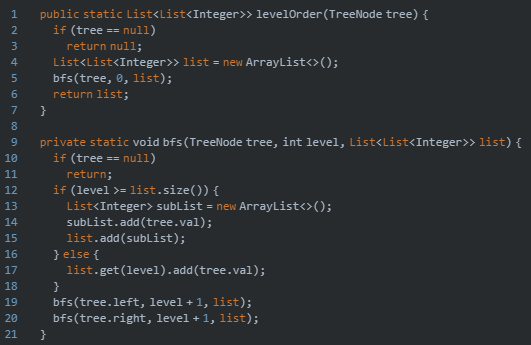
4,BFS(宽度优先搜索(又称广度优先搜索))
他的访问顺序是:先访问上一层,在访问下一层,一层一层的往下访问
所以上图前序遍历的结果是:A→B→C→D→E→F
访问顺序如下
代码如下
递归的写法

如果想把遍历的结果存放到list中,我们还可以这样写
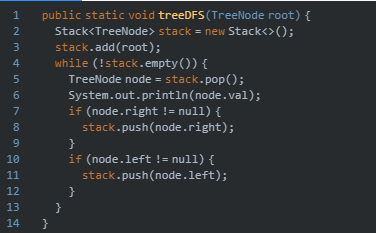
5,DFS(深度优先搜索)
他的访问顺序是:先访根节点,然后左结点,一直往下,直到最左结点没有子节点的时候然后往上退一步到父节点,然后父节点的右子节点在重复上面步骤……
所以上图前序遍历的结果是:A→B→D→E→C→F
访问顺序如下

代码如下
递归的写法